MATLAB学习笔记

常用命令

• quit: 退出命令

• clc: 擦除MATLAB工作窗中的所有显示内容，相当于命令行中的clear

• clf: 擦除MATLAB的当前图形窗中的图形

• clear: 清除内存中的变量和函数

• dir: 列出指定目录下的文件和子目录清单

• cd: 改变当前工作子目录

• disp: (在运行中)显示变量和文字内容

• who: 检查内存变量

• whos: 列出内存变量的详细情况

• save: 关闭前将变量保存到某一文件中

• load: 从之前保存的文件中恢复变量

• help: 非常有用

• lookfor: 查找相关指令

• !之后可以加操作系统命令，如 !ls, !vim

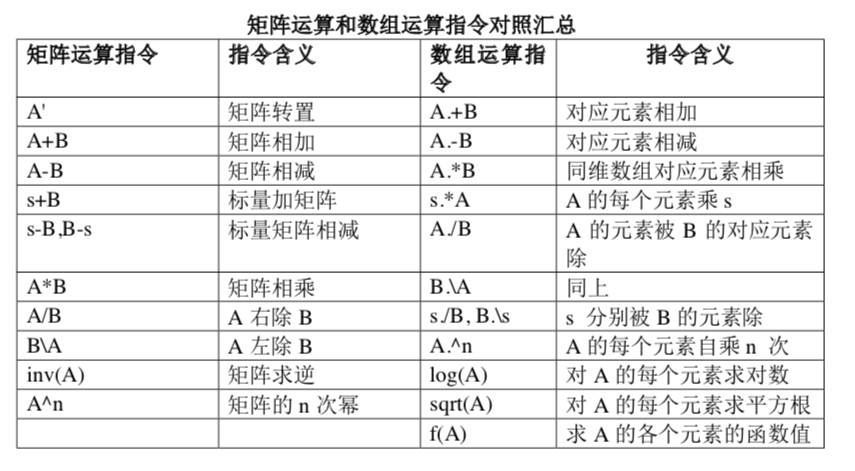
求解方程组时，用除法比用逆矩阵好。

多项式

• 用系数行向量表示：p=$[a_0 , a_1 , … , a_{n-1} , a_n ]$, ($p(x)= a_0 x_n + a_1 x_{n-1} + … + a_{n-1} x + a_{n} $).

• 可以用指令产生多项式系数向量: p=poly(AR). 如果AR是方阵，则多项式为特征多项式，如果AR为向量，则AR为多项式的解。

• poly2str函数

一些常用多项式运算指令

• R=roots(p) 求多项式向量p的根

• PA=polyval(p,S) 按照数组运算规则计算多项式值。 p为多项式，S为矩阵。 相当于求值。

• PM=polyvalm(p;S) 按照矩阵运算规则计算多项式值。p为多项式，S为矩阵。

• P=polyfit(x,y,n) 用n阶多项式拟合x,y向量给定的数据

数值积分

• S=quad(‘fname’,a,b,tol,trace) 自适用递推Simpson数值积分法

• S=quad8(‘fname’,a,b,tol,trace) 自适用递推Newton-Cotes数值积分法

• tol是精度，trace是是否画图

• quad8比quad有更高的积分精度

非线性方程求解

• 对于多项式函数求根，r=roots(p)

• 单变量非线性方程求解, z=fzero(‘fname’,x0,tol,trace)

• 一般非线性方程(组)求解， X=fsolve(‘fname’,X0)

文件读写

• fopen(“filename”,‘specifier’)

• fread(fd,..)

• fwrite()

• fclose

符号计算

• 可以用sym定义符号,如 sym(‘x’) 也可以用syms定义多个符号 syms a b c d

• findsym() 来确认符号表达式中的符号

微积分运算

• diff(f) 函数f对符号变量x或字母表上最接近字母x的符号变量求导数

• diff(f,t) 函数f对符号变量t求导数

• diff(f,2) 和diff(f,t,2)可以用来求二阶导数

• int(f)

• int(f,t)

• int(f,a,b) 和int(f,t,a,b)

• limit(f) 当符号变量x(或最接近字母x的符号变量) ->0 时，函数f的极限

• limit(f,t,a)

• limit(f,t,a,‘left’) 左极限 limit(f,t,a,‘right’)右极限

• symsum(s,t,a,b) 表示s中的符号变量t从a到b的级数和(t缺省时，同上)

• taylor(f,n,a) 函数f对符号变量x(或…)在a点的n-1阶泰勒多项式(n缺省时值为6，a缺省时值为0)

• solve(f,t) 对f中的符号变量t解方程f=0(t缺省值为x或…)

• solve(f,g,..)可以求解方程组

• dsolve(‘S’,‘s1’,‘s2’,…,‘x’)

• collect 合并同类项

• expand 将乘积展开为和式

• horner 把多项式转换为嵌套表示形式

• simplify 利用各种恒等式化简代数式，更强有力的函数simple

• subs(S,old,new) 替换

• subexpr(S) 将表达式S中的公共部分用sigma表示

MATLAB画图

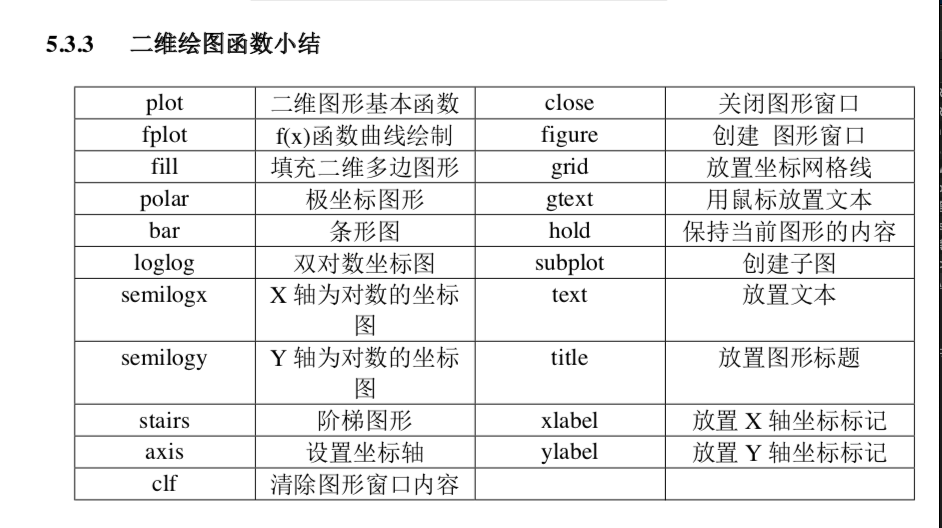
• plot(x,y) 以向量x作为X轴，以向量y作为Y轴，绘制X-Y二维曲线

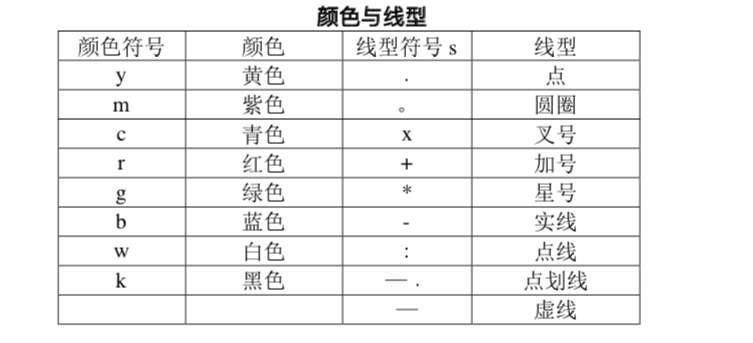
• plot(x,y1,‘k’,x,y2,‘b-') 每条曲线的线型和颜色由字符串’cs’指定，其中c表示颜色,s表示线型

• 可以加一些图形标记，如title, xlabel, ylabel, text,legend

• axis([xmin,xmax,ymin,ymax]) 来设定坐标轴范围

• hold on: 保持原有图形的基础上绘制新的图形

• fplot(fname,lims,tol) lims为变量取值范围，tol为相对误差

• loglog(x,y) 绘制双对数坐标图

• semilogx(x,y) semilogy(x,y) 绘制单对数坐标图

• polar(theta,rho) 用来绘制极坐标图

• plot3(x1,y1,z1,c1,x2,y2,z2,c2,…)

• mesh(x,y,z,c)绘制三维网格图

• surf(x,y,z) 绘制三维曲面图

• view 指定视点

• contour3 绘制等高线图

MATLAB程序设计

MATLAB有两种工作方式：一种是交互式的命令行工作方式，另一种是M文件的程序工作方式

M文件

M文件有两类：命令文件和函数文件。区别在于：命令文件没有输入参数，也不返回输出参数；而函数文件可以输入参数，也可以返回输出参数。

• input函数， A=input(提示信息，选项);

• pause(延迟秒数) pause()直接暂停程序

• Disp(输出项)

if选择语句

• 结束时要加end，不需要加begin

• else +if = elseif

switch语句

• 结束要加end

• default改为otherwise

• case 值 后面没有冒号

for循环结构

for 循环变量= 表达式1: 表达式2 : 表达式3
    循环体
end

% 表达式1为初值， 表达式2为步长，表达式3为终值

for 循环变量=矩阵表达式 则遍历矩阵元素

while循环结构

• 结尾加end

函数文件

function 输出形参表=函数名(输入形参表)
    注释说明部分
    函数体
    

• 当输出形参多余1个时，则应该用方括号括起来

• 参数可调， 用nargin和nargout实现

• 支持嵌套调用和递归

• 加global可以声明全局变量

参考资料：MATLAB 数学工具软件实例简明教程